International Conference. M. E. Kazarian – "xy swap duality in topological recursion"
Описание
International Conference, dedicated to the 75th birthday of Sabir M. Gusein-Zade
17.06.25
M. E. Kazarian (Moscow, Russia)
xy swap duality in topological recursion
The topological recursion or the Chekhov-Eynard-Orantin recursion is an inductive procedure allowing one to solve in a uniform way many enumerative problems. The initial data of recursion involves two meromorphic functions on a Riemann surface denoted usually by x and y. The xy swap relations relate solutions of two topological recursions with the roles of the x and y functions swapped. The very existence of such relations implies numerous applications clarifying the nature of topological recursion, in particular:
it leads to explicit closed formulas for the resulting differentials of the recursion in many cases that avoid the inductive procedure
it allows one to extend the recursion to the case of degenerate pairs of x and y functions and to analyze the dependence of the resulting differentials on x and y functions
it explains KP integrability property observed in many enumerative problems
The talk is based on a series of joint papers with A. Alexandrov, B. Bychkov, P. Dunin-Barkowsky, and S. Shadrin.
General information
The conference will be held in the Faculty of Mathematics of the HSE University (Usacheva str. 6, Moscow).
Dates: 16 - 20 June 2025
Organizers: A. Buryak, V. Medvedev, A. Skripchenko
More information:
https://math.hse.ru/modern_aspects_singularity_theory25/
https://mccme.ru/ru/modern_aspects_singularity_theory2025/
Автор

Похожие видео

Интерактивная игра «Юный финансист»

Как поставить палочку на клавиатуре

основные ошибки в работе оператором
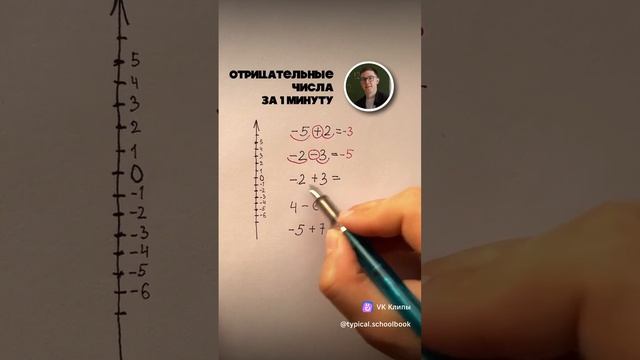
Сложение и вычитание чисел.

Мастер-класс по поступлению магистерской программы «Финансовые стратегии и аналитика»
Демонстрационные экзамены 2

26-Photography-JoelMeyerowitz-WhatIsStillLife-HD
